Introduction

This section of the error budget intends to describe the optical wavefront amplitude and phase immediately before M1 sufficiently well that the simulations of the internal properties of the VLTI can be de-coupled from simulations of the atmosphere. Also included in this section is a discussion of the beam walk at high altitude resulting from bulk atmospheric refraction, as this can be separated from the details of the atmospheric seeing simulations.

The simulations described in Section 3 were used to investigate the approximate level of perturbation introduced into the optical wavefronts by the atmosphere. One of the main complexities in the design and operation of PRIMA is the wavelength dependence of the wavefront corrugations across the telescope pupil, and the resulting wavelength-dependent perturbations to the fringe phase induced by atmospheric seeing (further details of this can be found in Section 28). This results from the wavelength dependence of the phase perturbations caused by atmospheric seeing which are described as a function of position in the AT aperture plane by Equation 17.

In order to illustrate the wavelength dependence of seeing effects, I have plotted various wavefront properties in the first timestep of the simulations. The wavefronts at M1 were not directly output from the simulations, only the resulting wavefronts after tip-tilt correction had been performed (subtracting the tip-tilt Zernike modes). Figures 7 and 8 show the delay applied to the wavefronts by the atmosphere after the tip-tilt correction. Figure 7 shows the case for $1.97\mbox{ $\mu$m}$ wavelength and Figure 8 the case for $2.43\mbox{ $\mu$m}$ wavelength. Note that apart from the pixel sampling in the images there is no obvious difference. This is because the delay $\Delta z$ from Equation 19 has only a weak dependence on wavelength.

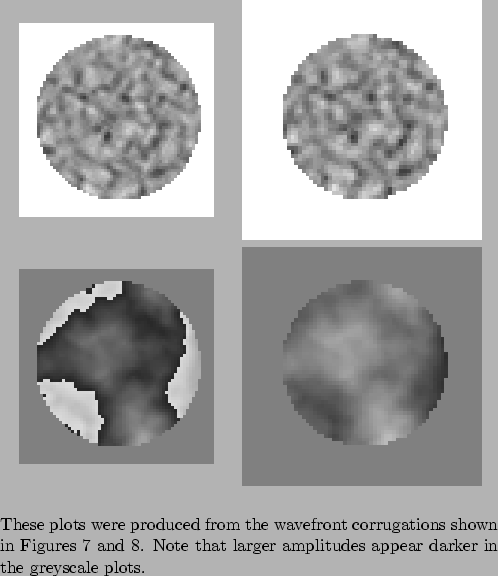
A larger difference appears when the atmospheric delays are converted into optical amplitude and phase. The amplitude and phase in the pupil plane are shown in Figures 9 and 10 for the same timestep as used for Figures 7 and 8. Figure 9 shows the amplitude and phase at $1.97\mbox{ $\mu$m}$ wavelength plotted as a function of position in the AT aperture plane. The discontinuities in the phase occur when the phase wraps around by $2\pi$ radians. The same plots are shown in Figure 10 for $2.43\mbox{ $\mu$m}$ wavelength. It is clear that the phase perturbations are much more severe at $1.97\mbox{ $\mu$m}$ due to the inverse relationship of the phase $\phi$ with wavelength seen in Equation 19.

	Figure 7 Atmospherically induced optical delay at one timepoint as a function of position in one AT aperture plane at $1.97\mbox{ $\mu$m}$ wavelength.	Figure 8 Optical delay at $2.43\mbox{ $\mu$m}$ wavelength at the same timepoint.

In both plots the tip-tilt Zernike modes have been corrected across the telescope aperture, resulting in a discontinuity at the edge of the aperture.

Figure 9 Optical amplitude (upper panel) and phase in the AT aperture plane at $1.97\mbox{ $\mu$m}$ wavelength. The discontinuities in the phase are due to the phase wrapping through $2\pi$ radians.
Figure 10 Optical amplitude and phase in the AT aperture plane at $2.43\mbox{ $\mu$m}$ wavelength.

Figure 11 Intensity in the image plane at $1.97\mbox{ $\mu$m}$ wavelength
Figure 12 Intensity in the image plane at $2.43\mbox{ $\mu$m}$ wavelength

Example plots from $4$ later timesteps of the simulations are shown in Figures 13 and 14.

Figure 13 shows the delay imposed on the wavefronts by the simulated atmosphere as a function of position in one of the AT aperture planes. The tip-tilt within the AT aperture has been corrected by perfectly compensating the tip and tilt Zernike modes, resulting in a discontinuity at the edges of the aperture in this plot. The four images show four timesteps with the atmospheric phase screens moving by $r_{0}/4$ in consecutive images in the directions described in Section 3. Each atmospheric layer has an equal effect on the wavefront phase.

Figure 14 shows the optical amplitude as a function of position in the same AT aperture plane. It is clear that the amplitude fluctuations are dominated by one of the layers moving from the lower left to the upper right. The dominant layer is the higher one ($5\mbox{ km}$ above the telescope - see Section 3.2).

Figure 13: The delay in the wavefront in the AT aperture at four timesteps after the tip and tilt Zernike modes have been corrected.
Figure 14: The corresponding optical amplitude in the AT aperture plane.