: Impact on astrometry : Refractive index of air : Error terms effected by 目次
If both the main delay line and differential delay line are filled
with air, then the measured distances within the VLTI must be
converted to OPD at the observing wavelength for each star. The
observing wavelength for each star is the centroid of the correlated
flux detected for that star. If the observing wavelength of the
primary star is ![]() , the observing wavelength of the
secondary star is
, the observing wavelength of the
secondary star is ![]() and the metrology wavelength is
and the metrology wavelength is
![]() , then the
, then the ![]() OPD measured at the laser wavelength
OPD measured at the laser wavelength
![]() is given by:
is given by:
We wish to measure ![]() :
:
The conversion from ![]() would be done using the best
estimates of
would be done using the best
estimates of
![]() and
and
![]() available. The
error
available. The
error
![]() in the differential OPD
measurement
in the differential OPD
measurement ![]() can be separated into a number of principle
terms:
can be separated into a number of principle
terms:
The error terms in Equations 25 and
26 can be further broken down by taking partial
derivatives. I will use the following approach:
| (27) | |||
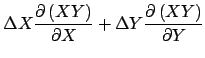 |
(28) |
Applying this approach to Equation 25 yields:
Typical values of the components making up these error terms are listed in Table 1.
| Term | Typical value | Units |
|
|
fractional error | |
|
|
|
 |
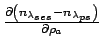 |
|
 |
|
|
fractional error | |
|
|
|
 |
 |
|
 |
|
|
||
|
|
|
 |
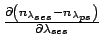 |
|
 |
|
|
||
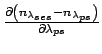 |
|
 |
|
|
Unknown in the near infrared | |
From Table 1 we can calculate approximate
magnitudes for the error terms listed in
Equation 30 for the air path in the DDL
If a reliable model for the refractive index of air can be
constructed, then it is clear that the error in the colour of the
observing band for the secondary star will dominate over the
contribution from air in the DDL, giving an total error contribution
of (summing errors in quadrature):
| (34) |
Equations 32 to 34 are listed
alongside a verbal description in Table 2.
| Equation | m |
|
| number | Description | per m air |
| 32 | The effect of |
|
| 33 | The effect of |
|
| 34 | The effect of a |
|
From Table 1 we can also calculate approximate
magnitudes for the error terms listed in
Equation 31 for the air path in the main delay line:
If the refractive indices of air and water vapour can be measured with
sufficient reliability, it is clear that the error in the colour of
the observing band for the primary and secondary stars will dominate
the contribution from air in the main delay line, giving a total error
contribution of (summing errors in quadrature):
| (39) |
Equations 36 to 39 are listed
alongside a verbal description in Table 3.
| Equation | m |
|
| number | Description | per m air |
| 36 | The effect of |
|
| 37 | The effect of |
|
| 38 | The effect of a |
|
| 39 | The effect of a |
|
Robert Tubbs 平成16年11月18日