Notes regarding this HTML version:
Depending on your browser and installed fonts, you might have some problems with certain characters in the text! However the display equations are in graphic format and will come through fine.

Coherent integration of fringe visibility in an optical stellar interferometer yields much higher signal-to-noise ratios in shorter integration periods for dim objects. Furthermore coherent integration, if performed simultaneously over multiple spectral channels, can yield direct determination of the phase of the visibility function, a quantity that is lost in incoherent integration.

To perform coherent integration it is necessary to estimate the random atmospheric delay to well within a wavelength. That determination can be used to compensate for the delay in hardware, or as a "phase reference" for integration of fringe visibility with the correction applied in software. This paper primarily addresses the latter method, and derives detailed corrections for the proper estimation of optical correlation given the interaction between the statistics of the incoming light and the hardware.

Of particular importance is the effect of error in the estimation of the atmospheric delay used as a reference phase. The author's previously published method for estimation of the atmospheric delay achieves well modeled error levels. In the case of very weak signals, even "ambiguous" determinations of atmospheric delay can be used for phase referencing. The delay estimator may employ the same raw data used for estimation of fringe visibility.

Aside from astrometry, the major goal of long-baseline optical stellar interferometry is the retrieval of image information through the precise measurement of optical correlation (fringe visibility) over a number of baselines. When there is a signal of sufficient strength to track the atmospheric delay t affecting the phase of interference, it is advantageous to perform coherent integration of V, the fringe visibility. As opposed to incoherent averaging of fringe visibility, one paramount advantage of coherent integration is the reduction of observation time in order to obtain a specified error level in the determination of V. This advantage is present for any observation in which the SNR received during a single integration period is much less than one⁴. This condition applies to dimmer objects, ones whose correlations are small to begin with, and/or measurements in which the number of detected photons is reduced by employing a narrow spectral channel.

A second advantage of coherent integration when multiple spectral channels are simultaneously processed, is that not only is the magnitude of V measured, but the phase of V is retained in the integration. This principle was illustrated in reference [5]. The ease with which coherent integration can accomplish phase determination of V as measured in adjacent spectral channels is verified by simulations which will be presented in this paper.

A further potential advantage of coherent integration is the reduction of systematic errors in the estimation of V, given that wideband tracking of the atmospheric delay removes ambiguity as to the location of the central fringe, and statistically defines the expected response of the integration procedure. If the atmospheric tracking mechanism can be well modeled in terms of its error statistics, analysis of the resulting system can yield correction factors which can refine the estimation of V. Details of several such correction algorithms comprise the bulk of this paper.

The issue of coherent integration really boils down to the time period over which photons can be accumulated so that the phase affecting the interference over that period is sufficiently stable, and the means to achieve that stability. An integration period much shorter than the atmospheric coherence time parameter T₀ will not be affected in magnitude by the atmospheric delay t. But since the phase of that observation is random, subsequent measurements of V cannot be averaged coherently. Instead it is necessary to average estimates of |V|² which we term incoherent integration.

Coherent integration can occur over a longer time period if the atmospheric delay is measured and compensated for in real-time using a delay-line with a sufficiently rapid response. Thus integration of photon detections for the estimation of V can occur coherently during a period of real-time fringe-tracking (or "fringed-locked") operation.

Alternatively, off-line delay tracking does not require high-speed delay compensation hardware. Instead, it is only necessary that raw data be acquired which is adequate for estimating the atmospheric delay function t(t). Then it is possible to use the determination of t for correction of the interference measurements in order to cancel the effect of the random atmospheric delay. These corrected measurements can then be integrated coherently (also referred to as "phase referenced averaging"^{3, 4}). In this case, with the correction performed in software, results are obtained similar to those obtained using hardware delay compensation.

The processing of raw data received using the hardware model depicted in Figure 1 in order to estimate V, is complimented by the author's previously published^{1, 2} method of estimating the atmospheric delay t using the same data stream. Refer to the signal flow diagram of Figure 2 in which the algorithm that estimates t is shown on the upper part of the diagram, and the estimation of V is shown on the lower part of the diagram. The estimation of V and t are mutually dependent inasmuch as the phase reference needed to integrate V coherently is supplied by the delay estimation algorithm (upper branch of Figure 2). However the algorithm which estimates t is itself benefitted by knowledge of the V(n) function provided by the lower branch. Thus the very best results will be obtained by estimating t(t), using that determination to coherently estimate V(n), and then repeating both processes.

Some features of the atmospheric delay estimation algorithm¹ may not be obvious. The achievable limit of estimation error derived in reference [2] is achieved by the proposed algorithm, with extended simulations producing estimation errors which match the theoretical curve within about 2%. That is important, because, as will be shown, coherent integration estimates of V are substantially affected by the exact rms error level in the estimation of t. Thus the delay estimation procedure supplies not only an estimate of that delay, but a close estimate of the rms error in that estimation. Secondly, at lower signal levels, the estimation of t(t) may not be a single function, but may consist of the union of several possibilities. An example of such an estimate is shown in Figure 8. Even though the estimation of t at a particular time is ambiguous, it is still possible to perform coherent integration by taking into account the range of possibilities. These and other nuances involving the coherent integration of V are detailed in the following sections.

Let us suppose that a photon of optical frequency n is detected in an interference channel in which the two optical signals are mixed with a relative phase of q. Furthermore let us assume that we have exact knowledge of the atmospheric delay. Let us call t the uncorrected component of atmospheric delay at the time of that photon's detection^*. We then define the detection phasor D as a function of n, q, and t:

Let t(t) be the uncorrected atmospheric delay as a function of time. Given a sequence of detected photons, for photon #k of optical frequency n_k which is detected at time t_k in an interference channel of mixing phase q_k, we will denote as D_k the absolute detection phasor for that photon:

Note that the absolute detection phasor is unobservable since t(t) cannot be known with precision. However we will analyze its characteristics as if it could be measured. We will then extend the analysis to versions of the detection phasor which are measurable.

In the special case that the uncorrected atmospheric phase shift 2pnt is totally random (uniformly distributed over [0,2p]), it can be shown that the expected value of the detection phasor is simply related to the fringe visibility:

Therefore if we were to select a subset of K photons whose optical frequency was n, we could average their detection phasors in order to form the following estimator of fringe visibility at the optical frequency n:

where we define the net detection phasor D_S as:This estimate derived from the detection phasor is the fundamental basis of any coherent integration scheme for determination of fringe visibility. Variations thereof are mainly distinguished by the means by which the estimate of t(t) is derived. If the estimate of the phase is solely derived from the same photons used in the formation of the detection phasor, then the phase of V is intertwined with the determination of the reference phase, thereby destroying any residual information regarding the phase of V, and allowing only for a determination of its magnitude. On the other hand, if there is an independent determination of the reference phase, then coherent integration using the detection phasor will return a complex number reflecting the phase of V. This can occur, for instance, if the reference phase is a result of atmospheric delay estimation based on light of other wavelengths.

The estimation error in using the detection phasor can be calculated in terms of the number of photons K which contribute to that estimation. As a worst case, we assume that the underlying V=0. Then the expected rms error in the estimation of the real part of V we denote as , which is given by:

The rms error of the imaginary part of the estimate is also given by . Although this error level applies exactly for the case of V=0, the error level in the case of non-zero V is similar, but slightly improved. However most of the corrections which will be discussed in the following pages increase the estimation error, but usually not by a large amount.

Therefore in order to attain an estimation of V having an error level of =.01, it would be necessary to base that estimate on about 20,000 detected photons. Figure 3 shows the result of estimating V using simulations in which about 5,000,000 photons were detected over 256 spectral channels. Thus each spectral channels received approximately 20,000 photons, leading to an rms error of about .01 in the magnitude of V, and to an rms error of about 1 in the phase of V (since the magnitude of V was .6 everywhere). Because this was derived from simulated data, it was possible to base the detection phasors D_k on exact knowledge of the atmospheric delay at the time of each photon, as stipulated in (2).

 

In a more realistic example, a wideband interferometer operating over a 2.5:1 wavelength range detects the underlying visibility vs. optical frequency function shown in Figure 4. That visibility curve describes a binary star consisting of a primary component modeled as a uniform disk which is itself resolved beyond the first null, and a secondary component having 5% the brightness of the primary, at a separation equal to ten times the diameter of the primary. Since the spatial frequency sampled is directly proportional to optical frequency, the effective baseline over which this system is observed also varies over a 2.5:1 range, observed as V as a function of wavelength as depicted in Figure 4.

In this case there were a total of 1,000,000 photons used in the estimation, or approximately 4000 per spectral channel leading to an expected error level of about .02 in the real or imaginary parts of V. The resulting estimation using the detection phasor is plotted in Figure 5 on top of the underlying model. Naturally the error in the phase of V is exaggerated when the magnitude of V is small.


Let us now examine use of the detection phasor to estimate V in cases where only estimates of t(t) are available, where the exact optical frequency n of a photon is only approximated by the spectral channel in which it was detected, and cases in which the assumption of a uniformly distributed random atmospheric phase is violated.

The above formula for the estimator (4), based on the expected value of the detection phasor given by (3), was dependent on the assumption of a random uncorrected atmospheric delay exp(-j2pnt) which is uniformly distributed around the unit circle. In the case of real-time delay tracking, this assumption may be violated. We will now examine modifications to (3) and (4) in order to handle the more general case.

We first introduce a modification to the definition of the detection phasor, previously given by (2), to include a minor correction factor:

In this expression, c is a small (<<1) correction function which will be detailed below.

Consider a photon of optical frequency n received at a time at which the uncorrected atmospheric delay was t, with underlying complex optical correlation V. Then in this more general case it can be shown that the expected value of the detection phasor (7) as now modified, would be:

In this expression, a and ß are parameters characterizing the photomixer and detector subsystem of the interferometer. In general they may be functions of optical frequency, even though it is not written explicitly in the following equations.

P₀(q) in (9) denotes the probability density of a photon which was detected, having been detected in a photomixer output with the mixing phase q, in the absence of optical correlation between the incident light waves (V=0). In the case of a discrete output photomixer, P₀(q) will consist of two or more delta functions and the integrals in (9) could be replaced by discrete summations. So if, under the condition of no optical correlation, p_i denotes the probability of a detected photon being found in the discrete photomixer output channel whose mixing phase angle is q_i, then a and ß would be given by:

a and ß are thus characteristics of the internal interferometer hardware and would not be expected to vary from observation to observation. They could be easily measured, for instance, by collecting data in which there is no possibility of optical correlation (for instance, one beam could be extinguished).

It should probably be pointed out that mathematically, a lossless photomixer would insure that a=0. However it still remains more than possible that the detector looking at one output phase could have a slightly different sensitivity than another, leading to a non-zero a. In the case that a is not zero, the correction function c in (7) will also be non-zero, and is defined as:

For certain ideal symmetric photomixer configurations ß will also necessarily be zero. However for the very important case of a balanced dual output photomixer (q₁= 0, q₂= 180°), ß=1. Therefore although the final (bias) term of (8) will usually be small, the second term may be very significant. In the extreme case of real-time delay tracking (t approx.= 0) using a two-phase photomixer (so that ß=1), we find that the instrument doubles its sensitivity to the real part of V, but becomes totally insensitive to the imaginary part of V. This is understandable, since interference is always being measured in the same mixing phase. That is why for a real-time delay tracking interferometer using a two-phase photomixer, it would be desirable to intentionally dither the delay of one beam in order to sample different phases of interference, as is commonly practiced.

Recall the net detection phasor D_S, defined in (5) as the sum of the detection phasors for photons received at the optical frequency n. Given the more general model and using (8), we compute the expected value of D_S as:

P₁ and P₂ are statistics derived from known (or estimated) values of t for the K photons:

Inversion of (12) then yields the maximum-likelihood estimator for V given the statistics D_s, P₁ and P₂ derived from the K detected photons:

For non-zero a, (14) is not a closed-form solution since the correction factors (1+c) in (7) are themselves dependent on the determination of V. This dependency may be resolved by first calculating the detection phasors (7) with c=0, and estimating V using (14). This estimated value of V may then be used to re-evaluate the detection phasors, and then re-estimate V using (14). Further iterations will not be required in most cases.

Since its denominator contains a statistic, it is not believed that the maximum-likelihood estimator (14) is, strictly speaking, an unbiased estimator. However it is a consistent estimator (that is, it approaches the actual value of V as K grows), and any bias is small compared to the rms error in cases in which the correction terms ( aP₁ and ßP₂) are not large. In special cases where the correction terms become dominant a different formulation would be appropriate. For instance, in the special case mentioned above of real-time delay tracking which insures that t0 at all times (so that P₁=P₂=K) and using a two-phase photomixer (so that ß=1), the numerator and denominator approach zero. For that particular case, inversion of (12) yields the following expression for the estimate of the real part of V:

If we assume there are not any striking spectral features inside the range of a wavelength channel centered about n₀, then we can presume that the actual optical frequencies of photons detected in that channel are uniformly distributed over [n₀-B/2, n₀+B/2], where B is the full optical bandwidth of the spectral channel. Then it can be shown that the first and second terms of the expected value of the detection phasor (8) will be degraded by a factor of sinc(Bt). In order to form an estimator with the least estimation error, one would also want to weight each detection phasor by sinc(Bt). Therefore we redefine the detection phasor D_k to be:

Then the expected value for the net detection phasor D formerly given by (12) would then be:

where the definitions of P₁ and P₂ have been slightly modified, and P₃ replaces K in the previous equation.

Note that the correction for finite spectral width is evaluated photon-by-photon, since the uncorrected atmospheric delay t and the resulting degradation in the expected amplitude of the detection phasor, varies for photons received at different times.

As before, we can create an estimate for V by inverting (17) to obtain an expression very similar to the previous estimate:

In addition to the substitution of P₃ for K in (14), we have redefined D_S, P₁, and P₂ above to take into account the finite spectral width of the detection channel.

The estimation of V using (19) will be degraded by the factor g which depends on the statistics of Dt. The estimator (19) for V must then be divided by this factor to correct for this degradation:

where:

In the particular case that the estimation error Dt is a zero-mean normally distributed random variable with an rms error of s_t, g will be given by:

As an example, the model for the binary star shown in Figure 4 was used to generate photons which were used to track t(t). The estimated t(t) function was then used to form the detection phasor for 1,000,000 photons in the estimation of V(n), or about 4000 photons per spectral channel. Without taking into account the degradation due to , the estimation of the magnitude of V, shown superimposed on the underlying function in Figure 6, is seen to be substantially diminished. We apply the correction using (21) and (23) with s_t=.201 femto-seconds, which is predicted for the signal level in question. The corrected results are shown in Figure 7.

While the correction contained in (21) will correctly compensate for estimation errors given a general statistical characterization of that error, we can do somewhat better if the delay tracking algorithm returns expected estimation error levels for estimates of t(t) at different times t. In that case, we would wish to find for each photon #k a specific to the estimation of t at the time of that photon:

Again, if the estimator of t(t) is known to be zero-mean and normally distributed, then g (24) may be evaluated using (23). Then in order to estimate V with the least error, each detection phasor must include a weighting factor of g_k, so that we would define the detection phasor as:

Using (25) and forming the net detection phasor D_S according to (5), we find that the expected value of D_S to again be given by (17), but with the following modified definitions of P₁, P₂, and P₃:

In general one could write the a posteriori probability density of t(t) for a particular t as:

Even when the estimate of t is characterized as the union of two or more gaussian densities, it is still possible to use that ambiguous estimate to coherently integrate fringe visibility using (19). In this case, however, we must accept the following more cumbersome form for the detection phasor of photon #k. We define the complex "strength" of photon #k as:

In (28) we have denoted the confidence of each estimate applying as p_i. The correction term c_i is given, for each possibility, by (11), thus:

Likewise the _i is given by (23) for each possibility:

where s_i is the rms error expected around the mean for the i^th possibility (in the case that they are specified as having different errors). Given the complex "strength" S_k of photon #k, the detection phasor D_k is expressed as:

Then it can be shown that the expected value of D_k is given by:

It is then possible to obtain the previous expression (19) for the resulting estimate of V, if we redefine P₁, P₂, and P₃ as follows:

In these definitions, p_ik and c_ik refer to those quantities applicable to the i^th possibility in the estimation of t(t_k) for the k^th photon. Note that it has now become necessary to include factors involving the correction function c(V,t) in the S_k and also therefore in the terms of P₁, P₂, and P₃. Thus repeated iterations to estimate V and update the correction factors, will now require recomputing these statistics as well as the net detection phasor.

We will now present two corrections in the estimation of V which are simply multiplicative factors to the result, and which don't require modification of the statistics contained in the estimator (21).

We assume that the two optical signals are combined in the photomixer with full wavefront matching, that is, they are both output in the same spatial mode. The process of limiting the light to a single spatial mode may introduce scintillation (intensity variations) in the light perhaps beyond that due to the small amount of scintillation initially introduced by atmospheric turbulence. Since these intensity variations would affect each beam separately, the intensities of the two optical signals being interfered will not generally match exactly. The measured amplitude of interference will suffer whenever the intensity ratio departs from unity.

For small to moderate intensity variations, it may be possible to model the intensity of either beam as log-normal, that is, the logarithm of the intensity will be described by a gaussian density with variance s_i². Let us assume that each beam has the same mean intensity, and each intensity varies independently with these statistics. We can ignore the temporal statistics of these variations as they will not affect the degradation in measured correlation over a period of time (assuming use of fast photon-counting detectors, as previously stipulated).

Then it can be shown that the measured fringe visibility will be degraded by the factor of exp(-4s_i²). Thus a corrected estimate of V would be given by:

where the raw estimate of V might have been computed using (21).

A final correction for the estimate of V is necessary to correct for detector dark counts or sky background . We will limit our scope to the case where, for a particular wavelength channel, receiving uncorrelated light (V=0), the ratio of signal counts to dark counts is approximately the same in all detector channels. This will be the case, for instance, if the p_i in (10) are approximately equal, and the array detector elements have the same level of dark counts.

If we measure the dark (or sky background) count level as being I_dark counts per second, and measure a count level of I_total when observing the object, then we can estimate the signal count level as being I_sig= I_total- I_dark. Then any measurement of V, for instance using (21), will be degraded by the factor I_sig/I_total. The corrected estimate would then be given by:

For a dark count level I_dark which is not small compared to the signal count level I_sig, there will also be a substantial increase in the error level in the estimation of V beyond that previously computed (6). In some cases a more important effect will result from the degradation in delay tracking performance due to the same decline in signal-to-noise ratio. Thus one would seek to employ detectors whose I_dark is at least somewhat smaller than the minimum I_sig level at which delay tracking could be performed.

Finally it should be mentioned that there may be additional phase factors not shown in Figure 1 affecting X₁ relative to X₂. Phase functions which are linear in describe achromatic delays, and are thus simply additive to t_e, the excess atmospheric delay. However non-linear phase shifts may occur as a result of material dispersion or other effects. For example if the delay-line in Figure 1 uses an air path, there will be a predictable dispersive phase factor introduced. Even if there is an optical dispersion compensation element designed to eliminate its effect, there may be a residual non-linear phase function remaining.

Let us call y(n) the non-linear phase shift affecting the first arm of the interferometer relative to the second. The interferometer assigns the correlation between the optical signals X₁ and X₂ to the underlying correlation V of the stellar source:

But if the underlying beams of starlight prior to the non-linear phase shift are denoted S₁ and S₂, then, neglecting common-mode phase shifts, we could write the received X₁ and X₂ in terms of S₁ and S₂:

The measured correlation would then be estimated to be:

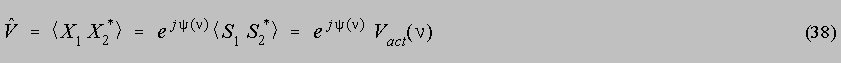
In other words, the phase of the estimate V will be rotated by the non-linear phase function y(n). The phase of V_act and y will be intertwined, and essentially inseparable. Thus to obtain meaningful measurements of the phase of V, it will be necessary to gain knowledge of y(n), the instrumental non-linear phase shift. It is expected that observation of a known symmetric object (arg(V)=0) may suffice for calibration, along with careful modeling of known variable dispersive effects, such as the dispersion due to the air in the delay-line as a function of the delay-line setting. Then the known y need simply be subtracted from the estimated phase of V to compensate for the known optical phase shift producing a corrected estimate for V:

Although this compensation will remove the bias in the determination of the phase of V, if the change in y(n) from one spectral channel to the next is not very small, it will reduce the amplitude of measured correlation in the same manner as that caused by a large uncorrected atmospheric delay for which we compensated using (16) and (18). Rather than using simply the uncorrected atmospheric delay in the correction factor sinc(B), we would need to rewrite these equations to compensate for the group delay d_g due to the y(n) function:

Then the corrections for the spectral channel width B in (16) and (18) would require the following modifications:

It has been emphasized that the spectrally-dispersed detection scheme depicted in Figure 1 will supply raw data that can both be used in the estimation of the atmospheric delay function t(t) and in the estimation of fringe visibility (correlation) V(n) as illustrated in Figure 2. Coherent integration of V is performed using the detection phasor (2) in which an estimate of t(t) is used as a reference datum to correct the phase of interference observed in the detection of a photon at time t. Unfortunately there is a certain bias introduced in the estimation of V in the case that the estimate of t used a random photon detection which is used as a phase reference for forming the detection phasor for the very same photon. That is because the estimation procedure for t is based on a figure of merit which seeks solutions under which the optical correlation would appear to be the greatest. Therefore the randomness in the detection of photons generates random errors in the estimation of t(t) which, for that specific raw data set, correspond to a greater magnitude of correlation than actually exists. At lower signal-to-noise ratios the effect of individual random photons on the estimation of t(t) is relatively greater, and this source of bias is therefore exaggerated. For instance, in Figure 10 at a low signal-to-noise ratio, the same photons were used in the estimation of t(t) and in the estimation of V, leading to a bias in the estimation of the magnitude of V. It can be seen that the bias has a greater effect on the estimation of V at higher optical frequencies (shorter wavelengths).

There is a straight-forward solution to avoiding this bias. If the estimate of t used in the determination of the detection phasor (2) for photon #k is based on every photon received except for photon #k, the source of the bias will have been removed. In principle that could be done for every single photon, so that every detection phasor integrated for the estimation of V will require a separate estimation of t. A more practical solution has been employed in the estimation of V(n) shown in Figure 11 in which the same raw data used in Figure 10 has formed an unbiased estimate of the underlying V. In this method the photons are arbitrarily divided into 4 sets. An estimation of t is performed using the photons in sets 2, 3, and 4, but in which the photons from set 1 are excluded. That particular estimate of t is then used to form the detection phasors for all the photons in set 1. Then sets 1, 3, and 4 are used to estimate t to apply to the estimation of V from set 2, and so on. In this way an unbiased estimate of V is formed on the basis of the entire set of detected photons. Beyond the increased computational burden^*, the elimination of one quarter of the photons increases the error in estimating t by about 10%, necessitating a larger correction for that effect (22).


 

We have seen that coherent integration of fringe visibility V may be implemented in one of two ways. Real-time delay tracking may be used to compensate for the excess atmospheric delay t_e in hardware, producing an optical signal in which the residual phase noise due to the atmosphere has been reduced to much less than a wavelength. Alternatively off-line estimation of the random atmospheric delay may be used to apply a correction phase factor to mathematically compensate for the effect of the uncorrected atmospheric delay function t(t) prior to averaging of the photons' statistics. Also known as phase referenced visibility averaging, this method yields results that are comparable to real-time tracking, but is somewhat more powerful since a superior estimate of t can be attained off-line using estimation methods such as detailed in references [1] and [2]. In order to avoid loss of coherence due to the uncorrected component of atmospheric delay over a detector element, it is necessary to still perform some level of hardware delay tracking and/or use a spectrally dispersed detection system in which the bandwidth of light falling on a single detector element is somewhat smaller than the reciprocal of the maximum anticipated uncorrected delay.

The effect of each photon detection with the phase correction for the estimated atmospheric delay, we have termed the detection phasor (1). In the most basic analysis, we have found that summation of the detection phasor (5) for photons of optical frequency n over the period of an observation yields a good estimate of V(n) according to (4). The estimation error of this procedure has been calculated (6) and falls off according the reciprocal of the square root of the number of photons integrated, as one would expect for coherent integration.

In cases where the atmospheric phase delay is not uniformly distributed around the unit circle, there are corrections that must be introduced to account for details of the interferometer's photomixing and detection hardware. These corrections summarized in the parameters a and ß (10), lead to the more cumbersome estimator for V (14). A further correction is introduced in (16) - (19) to account for the degree of incoherence in detection over a spectral channel as a result of a non-zero uncorrected atmospheric delay t, or the group delay (40) resulting from a non-linear function y(n) affecting the phase of interference, such as the dispersion caused by an air-filled delay-line.

While the accuracy of coherent integration is superb given exact knowledge of t as illustrated in Figure 3, apart from simulations, t can only be estimated. The magnitude of the resultant net detection phasor will be strongly dependent (22) on the error statistics of the estimator for t. Accurate compensation for the level of estimation error can be performed (21) based on knowledge of the level of that estimation error. Simulations using the author's delay tracking algorithms¹ have verified estimation errors that are very close to the theoretically predicted value. Therefore if such a delay estimation procedure is employed, not only will optimum correction of the phase of interference be applied, but knowledge of the estimation error in that procedure can accurately compensate for the degradation in the estimation of V due to the expected errors in the estimation of t.

It has been shown that for weaker signals not only does the rms error in delay tracking suffer, but the reliability (confidence) of estimates falls significantly below unity. Often falling under the category of "fringe-jumping," this effect is sometimes thought to limit the duration of coherent integration⁴. However it is in fact possible to take into account the net effect of "unreliable" estimates of t used as a phase reference in the determination of the detection phasor to the extent that the a posteriori probability density of t can be quantified. The resulting estimation procedure (28) - (33) can then be performed even in cases of very marginal signals for which delay-tracking can barely be performed.

[1] J. Meisner, "Atmospheric delay tracking in a long-baseline optical stellar interferometer", Optical Engineering, v. 35 #7 pp. 1927-1935, July 1996

[2] J. Meisner, Estimation and Tracking of Atmospheric Delay Noise in a Long-Baseline Optical Stellar Interferometer and Determination of the Expected Estimation Error, Ph.D. Thesis, University of Minnesota, 1995.

[3] D. Mozurkewich et al., "Phase Referenced Averaging as a Method for Decreasing the Variance of Visibility Measurements," NOAO-ESO Conference on High-Resolution Imaging by Interferometry, pp. 851-854, 1988.

[4] A. Quirrenbach, D. Mozurkewich, D. F. Buscher, C. A. Hummel, J. T. Armstrong, "Phase-referenced visibility averaging in long-baseline interferometry," Astronomy and Astrophysics, v. 286, pp. 1019-1027, 1994.

[5] D. Morancais, P. Nisenson, "Phase Reconstruction in Optical Interferometry," Optics Communications, v. 67 #1, pp. 39-44, 1988
 
 

Textual Footnotes:
* In relation to Figure 1, the uncorrected component of atmospheric delay t is the difference between t_e, the excess delay in one arm of the interferometer caused by the atmosphere, and t_c, the correction delay which may optionally be applied to the delay line in order to partially compensate for t_e.

* It should be pointed out that this method does not quadruple the computational burden in the estimation of t. That is because, in the most computationally intensive cases arising from low signal-to-noise ratios which produce multiple path solutions such as shown in Figure 8, the bulk of the computation involves finding the general topology and location of the various paths. That can best be done using all of the detected photons. Then using that estimate as a starting point, the removal of one quarter of the photons requires only a relatively simple recalculation of the precise mean position and confidence for each path.